Two versions of FF competed in the 3rd International Planning
Competition:
As said, we give gnuplots for the runtime and solution length data
gathered in the competition. We start with the STRIPS domains, then
focus on the numerical domains. For both FF-v2.3 and Metric-FF there
also participated a FF.quality version which favored solution
quality in the sense that it used an estimate of the remaining cost
(the cost of the relaxed plan, cost in the case of Metric-FF
possibly being a linear function over the numerical variables) in a
standard A* algorithm. We only show the data for the classical
FF.speed versions, which use relaxed plan length as a goal
distance estimate in a variation of Hill-climbing (see the respective
individual pages and papers). In a similar fashion, we only include
data for the versions of MIPS and LPG that favored speed over
quality. Runtime is always shown on a logarithmic scale. Data points
for unsolved tasks are ommitted from the plots. The data are largely
self-explanatory so we do not include much explaining text. Note
that we are not trying to analyze the competition results. The only
claim is that FF's performance was top in those domains where it
participated.
STRIPS DOMAINS
NUMERICAL DOMAINS
Both systems demonstrated top performance across the domains in which
they participated, i.e. in the case of FF-v2.3 the STRIPS domains, and
in the case of Metric-FF the (purely) numerical domains. On this page,
we give gnuplot graphics showing the data concerning the runtime taken
in these domains, as well as the data concerning the number of actions
in the found plans. In all domains and with regards to both criteria,
the FF systems are among the two or three top performers, and in some
domains FF outperforms all other competitors significantly. The
systems have not been chosen for an award due to the broader coverage
of some other competitive systems, i.e. because FF did not deal with
the durational constructs in the competition. As is orthogonal to
broad coverage, our philosophy in development was / is to take our
time and do extensions step by step, rather than trying to do it all
at once. On the negative side, FF can not yet solve durational
planning tasks. On the positive side, Metric-FF
is a scientifically satisfying approach to deal with numbers (the
heuristic function approximates the goal distance of a state in a
fashion that combines the logical and numerical apsects of
the task), and achieves excellent results across a range of benchmark
domains.

1.a) Depots-Strips runtime, shown on a logarithmic
scale. Generally, FF is fastest together with LPG and Simplanner; some
of the smaller tasks require exceptionally much runtime.
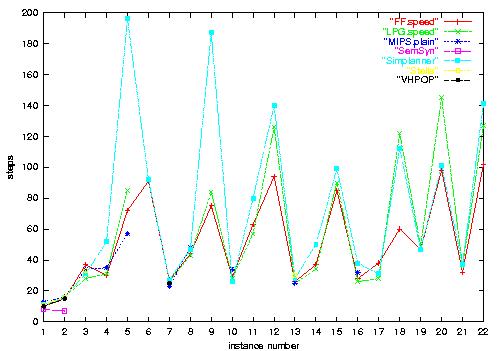
1.b) Depots-Strips plan length. LPG and in
particular Simplanner sometimes find overlong plans; FF's plans tend
to be shortest.

2.a) Driverlog-Strips runtime, shown on a
logarithmic scale. LPG and FF are most efficient, LPG scales somewhat
better to the largest tasks.

2.b) Driverlog-Strips plan length. Plan lengths are
roughly similar for all planners.

3.a) Zenotravel-Strips runtime, shown on a
logarithmic scale. FF outperforms the other planners.

3.b) Zenotravel-Strips plan length. FF's plans tend to be shortest.

4.a) Satellite-Strips runtime, shown on a
logarithmic scale. LPG, FF, and Simplanner tend to be fastest.
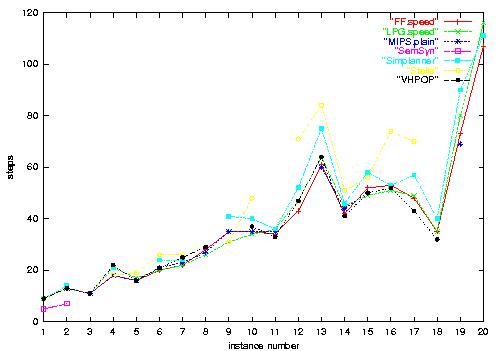
4.b) Satellite-Strips plan length. Plan lengths are
roughly similar for all planners.

5.a) Rovers-Strips runtime, shown on a
logarithmic scale. FF outperforms the other planners.
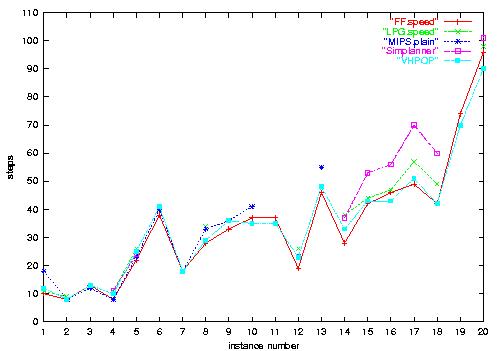
5.b) Rovers-Strips plan length. Plan lengths are
roughly similar for all planners.

6.a) Freecell-Strips runtime, shown on a logarithmic
scale. FF is generally the fastest, followed by LPG and MIPS.
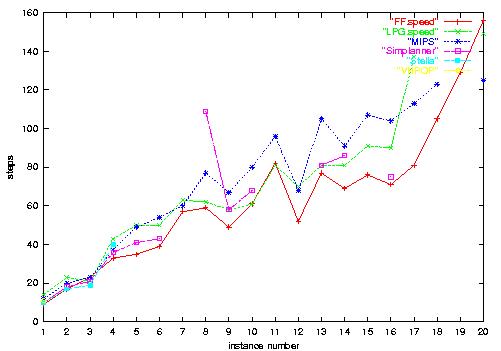
6.b) Freecell-Strips plan length. FF tends to find
the shortest solutions.
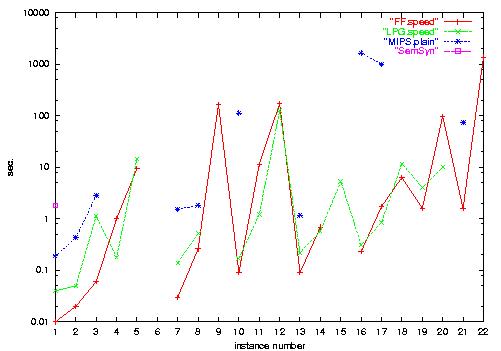
1.a) Depots-Numeric runtime, shown on a logarithmic
scale. FF and LPG are most efficient.
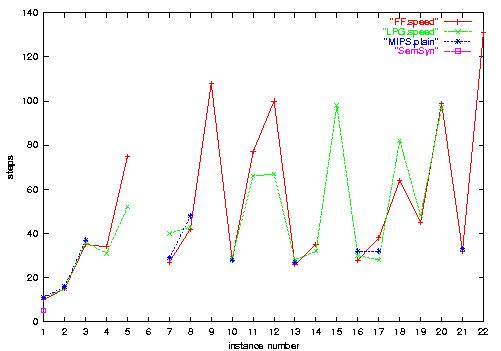
1.b) Depots-Numeric plan length. No planner is
clearly superior in solution length.
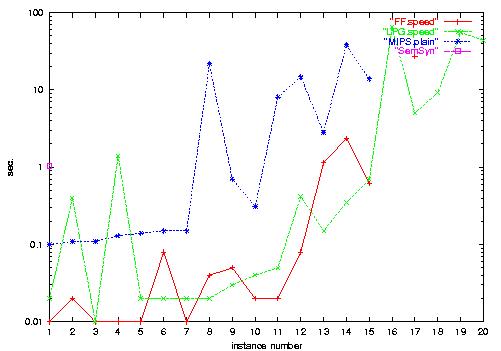
2.a) Driverlog-Numeric runtime, shown on a
logarithmic scale. LPG is most efficient, followed by FF and MIPS.
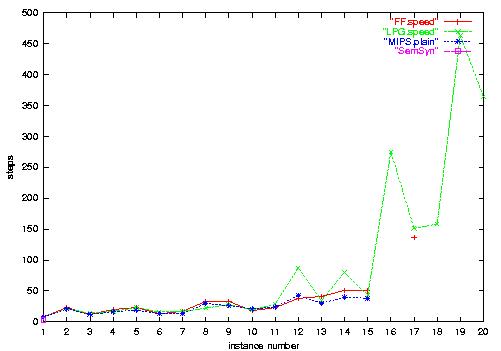
2.b) Driverlog-Numeric plan length. Plan lengths are
roughly similar for all planners.

3.a) Zenotravel-Numeric runtime, shown on a
logarithmic scale. FF is most efficient.
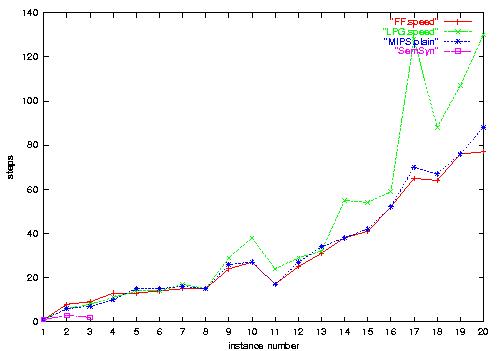
3.b) Zenotravel-Numeric plan length. FF's and MIPS
plans tend to be equally long, LPG's are longer.
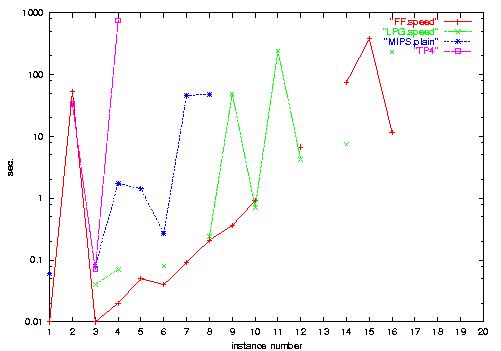
4.a) Satellite-Numeric runtime, shown on a
logarithmic scale. LPG and FF are most efficient.
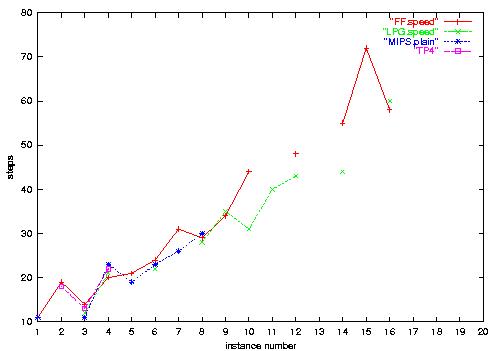
4.b) Satellite-Numeric plan length. Plan lengths are
roughly similar for all planners.
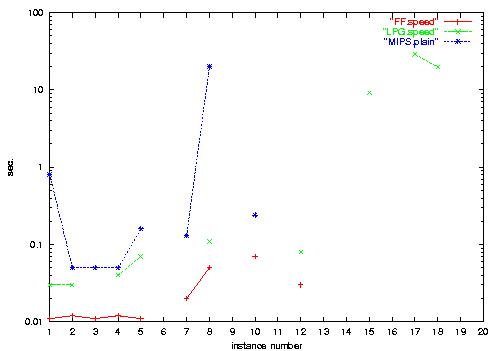
5.a) Rovers-Numeric runtime, shown on a logarithmic
scale. FF is slightly more efficient in the smaller instances, but LPG
is the only approach that can solve some of the larger tasks.
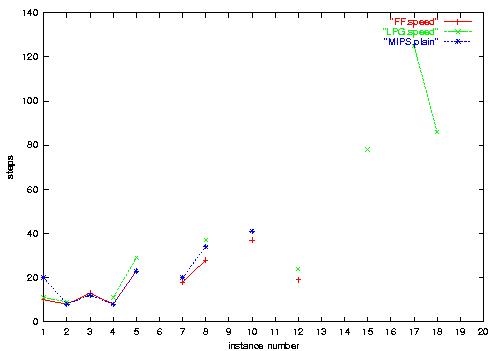
5.b) Rovers-Numeric plan length. Plan lengths are
roughly similar for all planners.
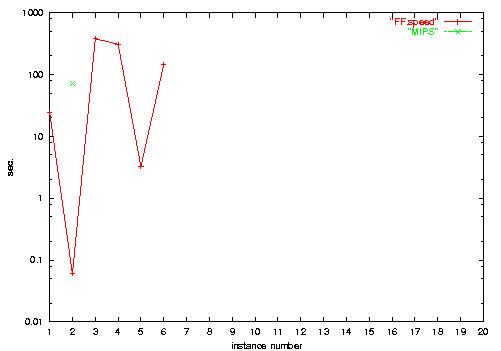
6.a) Settlers-Numeric runtime, shown on a
logarithmic scale. MIPS can solve only a single instance,
Metric-FF solves the smallest 6 tasks; LPG couldn't be run here as
there appear universally quantified effects. We remark at this point
that Settlers, of the domains in the competition, is the one that uses
the numerical variables most extensively; so this might be a domain
where Metric-FF's heuristic function, which integrates the numerical
values into its estimation process, pays off (though FF can not solve
all of the, rather large, competition instances).
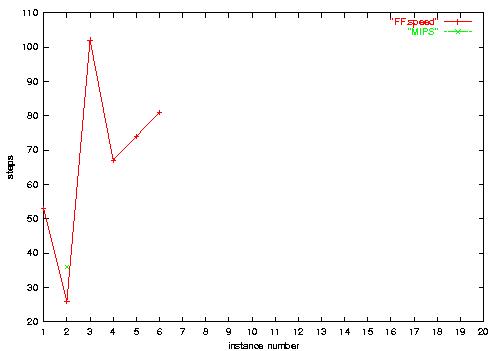
6.b) Settlers-Numeric plan length. In the
single task that MIPS can solve, FF's plan is somewhat
shorter.